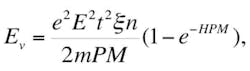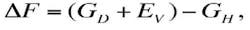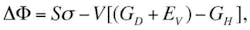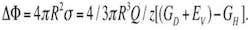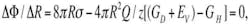It is well known that the crystallization process directly impacts the structure of an alloy, which determines its mechanical properties. Therefore, energy’s influence on the process of crystallization has high practical importance, because it allows improvement in the steel grade and decreases the mass for casting. As factors of influence on metal alloys before filling the mold one may use different physical fields, including an electric field1.
To determine the efficiency of processing of liquid alloys by electric field, experiments on cast steel with carbon content of 0.4% were conducted. Processing was done with wolfram electrodes immersed into the steel melt under the following conditions: current density 0.970 A/cm2, processing time 60 sec. This regimen was chosen using practically obtained dependencies of the increment of the tensile strength ΔσB=16[1–exp(-5.08i)] and the increment of limit value of fluidity of alloy ΔσT=11[1–exp(-3.96i)], where i is current density.
In the process of measuring of the influence of the electric field on the crystallization process, special cone copper molds were used, with a height of 60 mm, upper diameter of 40 mm, and lower diameter of 30 mm. Steel was produced in an induction furnace with a volume 160 kg, with a refractory lining, and under temperature (1,500±10)°C it was transfused in two casting ladles of volume 40 kg. The steel melt was kept in ladles for 60 seconds, and one of them was under an influence of electric field.
Then, both kinds of steel were poured into two metal forms, where after a three-second delay there was “freezing” of steel crystals on the walls of the forms. After that the liquid residue steel was poured from forms into a mold. The crystal steel castings thus obtained were removed from the metal molds, and 10-mm high ring samples were cut out at a distance of 20 mm from the bottom of castings. These ring samples are shown in Figure 1.
Measurements of the thickness of samples of “frozen” steel crystals showed that on the samples processed by electric field the thickness is larger than on the samples of initial steel. The difference between these values obtained using 27 experiments, on average, occurred to be equal to 6.70 mm. These results prove that the energy of crystal elements of steel is essentially decreased and the number of centers of crystallization in a volume unit of liquid steel is increased after processing by electric field. The increase in the number of crystallization centers results in increasing of the number of equiax crystals, which appear on the first stage of crystallization under a contact with metal walls of forms. These changes in the parameters of the crystallization process lead to increases in the thickness of the ring samples of the processed steel.
To explain this phenomena, a physical model was built of the interaction of electrons which are accelerated by the electric field in the interelectrode space, with atoms of fluid alloy, which are located near centers of crystallization, based on the Drude-Lorenz theory2. Then energy of electrons Ev transmitted to the atoms of alloy is equal to
where e is the electron charge, accelerated by an electric field; E is the electric field; t is the average time between collisions of electrons with the centers of crystallization and crystal elements of alloy; ξ is a coefficient (ξ < 1), reflecting the number of electrons interacting with the centers of crystallization and crystal elements of alloy; n is the total number of electrons in the interelectrode space; m is mass of electron. H is the distance between the electrodes immersed in the molten alloy; P is the sectional area of the nucleation and crystal elements of alloy; M is the number of centers of crystallization and crystal elements of alloy in electrode layer of melt having volume X + dX.
Values of this ratio show that for sufficiently large numbers of crystallization centers M and values of P, the value (1-e-HPM) tends to 1. The total energy E3 of electrons transmitted to the crystallization centers is directly proportional to E2, i.e. to the amount of Joule heat produced in the interelectrode space. As the transfer of the electron energy grows more intensive, the greater is the number of crystallization centers and elements of crystal alloy and their total cross-sectional area perpendicular to the flow direction of the conduction electrons.
The effect of the impact of the electric field on the crystallization process of cast steel may be explained by the fact that the transmission of energy of electrons to atoms of the boundary layer of crystallization centers increases the free energy in a local volume of alloy near the center. This leads to an increase in the difference of free energy of liquid and solid phases of alloy ΔF, that is,
where Q is the molecule mass of alloy; z is the density of alloy. Therefore, R=2σQ/[(GD=GH]z , while R’=2σQ/[(GD=GH]z, where R’ is critical radius of elements of original, non processed alloy.
Comparing equations for, R, R’ , we conclude R’>R.
Thus, the impact of the electric field on the process of crystallization of foundry alloy changes the conditions of this process and, as experiments show, give an option of positive influence on the number of crystallization centers in a unit volume of the melt. This change in the number of crystallization centers makes the structure of the alloy more fine-grained, which improves its mechanical properties. This influence, undoubtedly, decreases the weight of the cast and, consequently, allows a decrease in its cost and increases the profitability of production.
Dr. Minenko is an associate professor and head of the Resource Center for the Ministry of Industrial Engineering Education, Moscow. Contact him at [email protected]
REFERENCES
1. Minenko G.N. “Factors Influencing Electric Field Treatment for Alloy Modification,” FM&T, July 2014, p. 22-23.
2. Minenko G.N., Smirnova Yu.A., “Physical model of the influence of electric current on the crystallization process of the alloy,” Metallurgy Engineering, 2009, No. 3, p. 48-49.